The Superformula is an equation that is an extension of the both of the sphere and ellipse equations, with this geometrical approach is possible to module and understand various abstract, natural and artificial shapes, so starting from the concept of the circle is possible to describe a large variety of shapes. This formula was proposed by Johan Gielis around 2000, the formula was obtained by generalizing the super ellipse, created by Piet Hein, a Danish mathematician.

In polar coordinates with $r$ the radius and $\phi$ the angle, the superformula is:

$$r(\phi) := \frac{1}{\left\{ \left[ \left( \left| \frac{1}{a}\cos(\phi\frac{m}{4}) \right| \right)^{n_2} + \left( \left| \frac{1}{b}\sin(\phi\frac{m}{4}) \right| \right)^{n_3} \right]^{-\frac{1}{n_1}} \right\}} \qquad \qquad (1)$$

It’s possible to generate different shapes choosing distinct values where the parameters $m$, $n_{1}$, $n_{2}$ and $n_{3}$ are real numbers and $a$, $b$ are real numbers excluding zero. When $n_{1}=n_{2}=n_{3} = 2$, $m = 4$ in equation 1, an ellipse is obtained. A circle is obtained when additionally, $a=b$.

The equation 1 is defined in 2 dimensions, but is possible to extend the superformula to 3, 4 or $n$ dimensions via the spherical product of superformulas, so whether we focused on a 3D space, it’s possible to obtain a 3D parametric surface multiplying two superformulas $r_{1}$ and $r_{2}$, the 3D coordinates are described with the following relations:

$$\begin{aligned}x = r_{1}(\theta)\cos(\theta)r_{2}(\phi)\cos(\phi)\\y = r_{1}(\theta)\sin(\theta)r_{2}(\phi)\cos(\phi)\\z = r_{2}(\phi)\sin(\phi)\end{aligned}$$

Where latitude is represented between $-\pi/2\le\phi\le\pi/2$ and longitude between $\pi\le\theta\le\pi$.

With these relations shown above, we can map it onto a spherical topology, but could be possible to map it onto different topologies such as a toroidal mapping, for example. To reach it, in 3D coordinates would be described with the following relations:

$$\begin{aligned}x = \cos(\theta)\left[r_{1}(\theta)+r_{2}(\phi)\cos(\phi)\right]\\y = \sin(\theta)\left[r_{1}(\theta)+r_{2}(\phi)\cos(\phi)\right]\\z = r_{2}(\phi)\sin(\phi)\end{aligned}$$

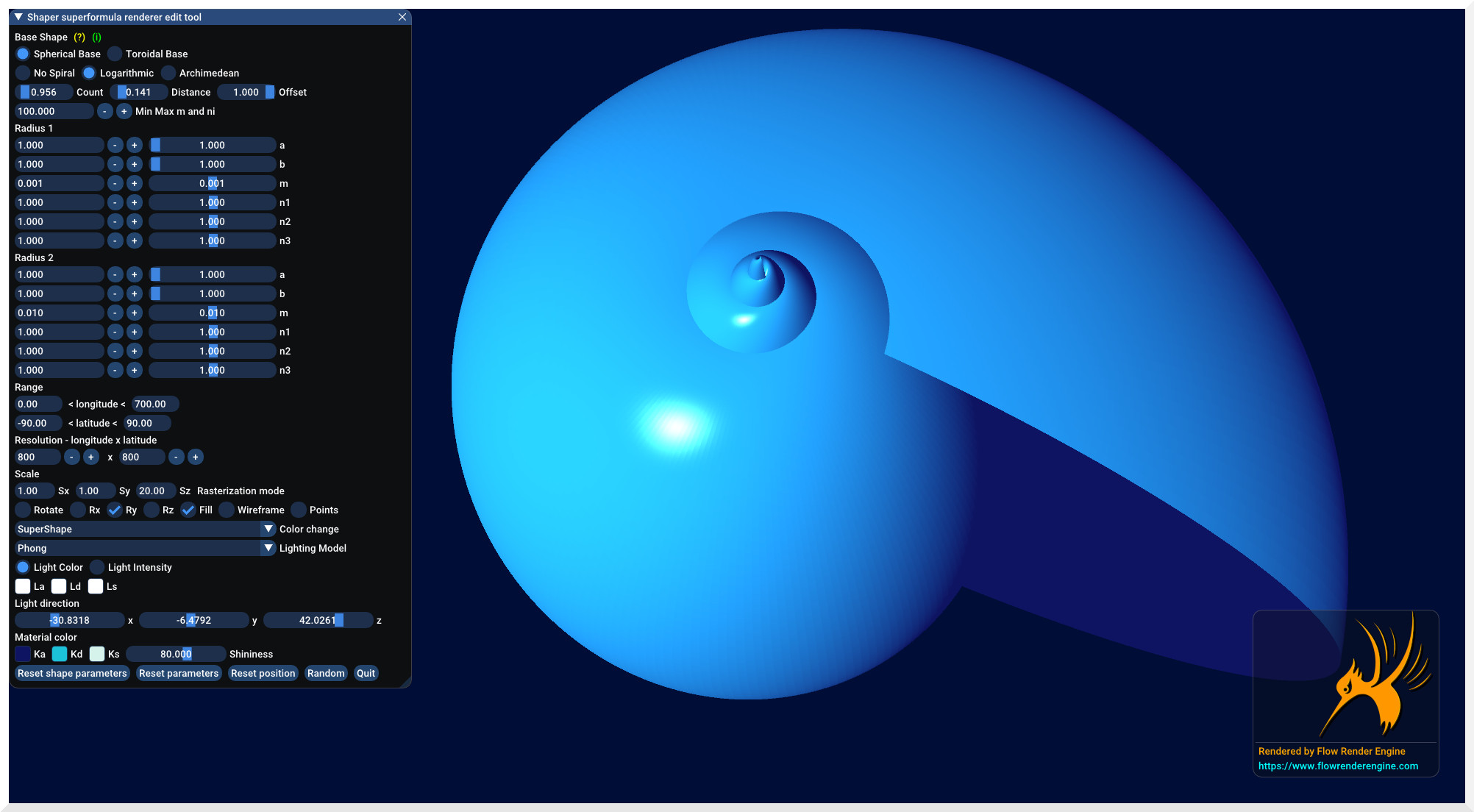
Shaper supershapes superformula tool

The Shaper superformula is a tool developed over Flow render engine written in C++, that implements the superformula as described above mapping onto a spherical and toroidal topology and modulated by a logarithmic and Archimedean spiral within a 3D space, it being possible to explore different shapes with this tool.

The tool published here, is the Webassembly version build via Emscripten from original code written in C++ so, it exists a desktop version of the tool that runs on Windows and Linux, but for the moment is not available.

Main Features

• Exploring different 3D shapes by either single parameter ranges or simply choosing a random parameter set.
• Spherical and toroidal 3D mapping with logarithmic and Archimedean modulation.
• One shape can be morphed to another modifying the parameters manually.
• Different rasterization modes such as wireframe, point and fill.
• The shapes can be rendered with Phong, Blinn, Lambert and Gouraud shading models with several colour ramps.
• Shapes in low, medium and high poly can be generated and rendered, modifying the resolution defined by longitude x latitude.
• The shapes can be translated, rotated, scaled and zoomed during the exploration.
• Screenshots can be taken and downloaded in PNG format.

Next improvements

• Waveform OBJ Exporter/Importer to save and retrieve the supershapes.
• OpenCL support in desktop version for faster GPU buffer updates.
• Improvements in background, it’s only able to change the background colour for now.
• New shading models implementation.
• GUI improvements.
• Improvements in morphing transition control.

The following images depicts some abstarct and nature shapes generated with the tool.

External links

Superformula

Gielis, Johan(2003), A generic geometric transformation that unifies a wide range of natural and abstract shapes

Paul Bourke Supershapes